Binary Search

Purpose:

Find an element in a sorted list of elements

Logic:

In a sorted list, look at the middle element and then you only have to search to your left of right, halving the search space. Repeat this in a loop, on each iteration the search space is halved.

Condition:

List must be sorted in either increasing or decreasing order

Algorithm:

Use 3 pointers for start, end and middle indices of the list
Loop until start index is less than end index
Check middle element if equal to target element
If list sorted in increasing order
1. If middle element greater than target, look to the left
  1. Set end = mid-1 and mid = (start+end)/2
2. If not, look to the right
  1. Set start = mid+1 and mid = (start+end)/2
If list is sorted in decreasing order
1. Just reverse the comparison in Step 4.1 and look to the right

Code: Iterative

// returns index elem was found at and true if found and no of searches required
func binarySearch(arr []int, target int) (int, bool, int) {
	var start, end, mid, searches int
	end = len(arr) - 1
	mid = len(arr) / 2

	for start <= end {
		searches++
		if arr[mid] == target {
			return mid, true, searches
		}
		
		// if increasing order of elements "<" else ">"
		if arr[mid] < target {
			start = mid + 1
		} else {
			end = (mid - 1)
		}
		mid = (end + start) / 2
	}

	return 0, false, searches

}

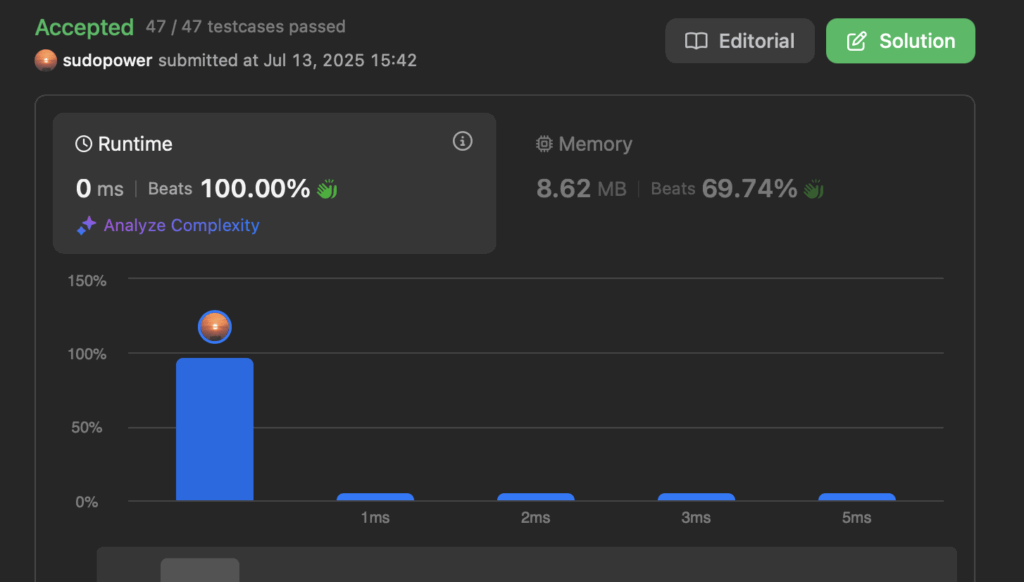
Code: Recursive

func binarySearch(arr []int, target, start, end int) int {
    if start>end{
        return -1
    }
    mid := start + (end-start)/2
    if arr[mid] == target {
        return mid
    }
    
    if arr[mid] < target{
        return searchRecursive(arr,target,mid+1,end)
    } else {
        return searchRecursive(arr,target,start,mid-1)
    }

    return -1
}

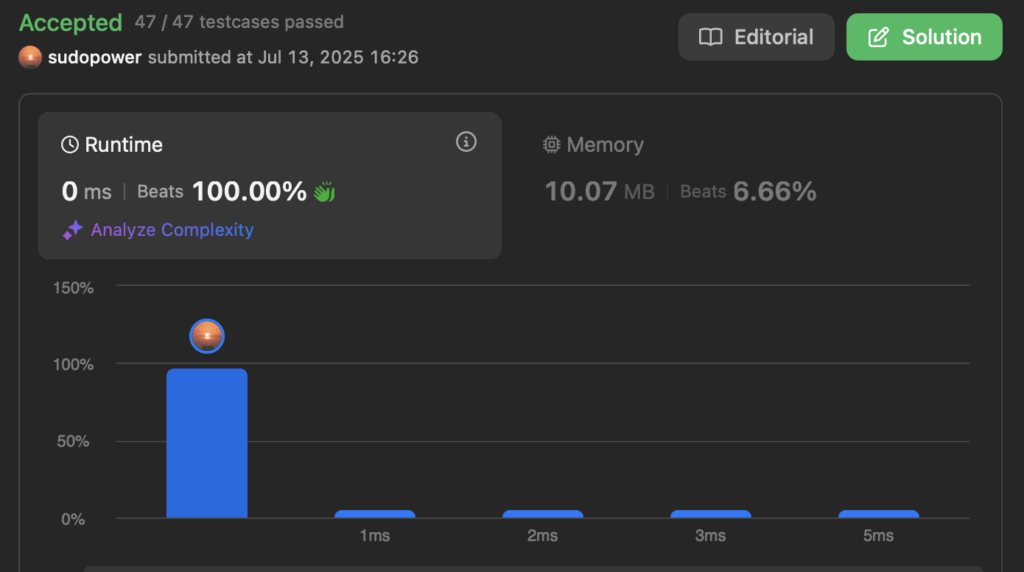
Test:

IP: arr=[1,2], target=2
OP: found at: 1 searches: 1 

IP: arr=[1,2,3,4], target=4
OP: found at: 3 searches: 2 

IP: arr=[1,2,3,4,5,6,7,8], target=8
OP: found at: 7 searches: 3

IP: arr=[1,2,3,4,5,6,7,8,9,10], target=10
OP: found at: 9 searches: 4

IP: arr=[1,2,3,4,5,6,7,8,9,10,11,12,14,14,15,16], target=16
OP: found at: 15 searches: 4 

IP: arr=[1,2,3,4,5,6,7,8,9,10,11,12,14,14,15,16.....32], target=32
OP: found at: 31 searches: 5

Time and Space Complexity:

// returns index elem was found at and true if found and no of searches required
func binarySearch(arr []int, target int) (int, bool, int) {
	var start, end, mid, searches int			// 1 time and 4 space units
	end = len(arr) - 1							// 1 time 
	mid = len(arr) / 2							// 1 time	

	for start <= end {							// k+1 times, 0 space
		searches++								// everything inside k times, no extra space
		if arr[mid] == target {					
			return mid, true, searches
		}

		if arr[mid] < target {
			start = mid + 1
		} else {
			end = (mid - 1)
		}
		mid = (end + start) / 2
	}

	return 0, false, searches 					// 1 time, 0 space

}


/*
Space Complexity: O(1) - no additional space is used that grows with input size

Time Complexity: 
Lets trace the values of k for and find an expression for the time complexity.
for n=2 worst case k = 1
for n=4 worst case k = 2
for n=8 worst case k = 3
for n = 10 worst case k = 4
for n = 16 worst case k = 4
for n = 32 worst case k = 5

n = 2^k
k = log2(n)
*/

Time complexity: O(log₂n)

Space complexity: O(1) excluding input

Try it : Link

// You can edit this code!
// Click here and start typing.
package main

import "fmt"

func main() {
	target := 32
	var arr []int
	for i := range target {
		arr = append(arr, i+1)
	}
	if idx, found, searches := binarySearch(arr, target); found {
		fmt.Printf("found at: %d searches: %d ", idx, searches)
	} else {
		fmt.Println("not found")
	}

}

// returns index elem was found at and true if found and no of searches required
func binarySearch(arr []int, target int) (int, bool, int) {
	var start, end, mid, searches int
	end = len(arr) - 1
	mid = len(arr) / 2
	order := arr[start] < arr[end]

	for start <= end {
		searches++
		if arr[mid] == target {
			return mid, true, searches
		}

		// if increasing order of elements "<" else ">"
		if (order && arr[mid] < target) || (!order && arr[mid] > target) {
			start = mid + 1
		} else {
			end = (mid - 1)
		}
		mid = start + (end - start) / 2 // since start+end can exceed integer range for large inputs
	}

	return 0, false, searches

}